Huhu ihr Freunde der Zahlen =)
Ich habe aufgrund eines Aufgabenkomplexes (dessen Lösung zu meinem Leidwesen benotet wird) einige Dinge festgestellt, die mir sehr schwer fallen, einerseits, weil ganz grob gesagt meine letzte Mathelehrerin nicht so ganz das Gelbe in der Sahnesoße war und ich zweiter für vieles auch einfach kein Vorstellungsvermögen habe^^".
Grob gesagt geht es im Moment erstmal nur um Zahlenfolgen:
a) habe ich hier eine Aufgabe, in der ich die Anzahl derjeniger Glieder der Folgeberechnen soll, die außerhalb von ε-Umgebung von g liegen, wobei ε = 10^-5
Nun habe ich bereits g aufbestimmt, habe aber überhaupt keinen Anhaltspunkt, wie man die Anzahl der Glieder außerhalb von ε bestimmen könnte, zumal wir außer der Tatsache, dass ε eben der Bereich um g ist, in dem unendlich viele Glieder liegen und eben endlich viele außerhalb davon, nichts darüber erfahren haben (das sei den L-Kursen vorbehalten !_!).
b) habe ich nie so wirklich geschnallt, wie die Sache mit den Logarithmen funktioniert, geschweigedenn, die Gesetze (die wir uns meines Wissens nach auch nicht aufgeschrieben haben). Ich komme mit Müh und Not immer auf die Tatsache, dassin
umgewandelt wird. Es geht aber schon bei der Eingabe in den Taschenrechner los, dass ich nicht schnalle, wie man beispielsweise
mit dem Zehnerlogarithmus ausrechnen kann, wobei ich jetzt sogar glaube, mir erknobelt zu haben, dass das
sein müsste (auch, wenn mein Taschenrechner ein log statt lg anzeigt).
Eine kleine Reaktion wäre also sehr schön, zumal das ganze sich anscheinend auf Abiniveau bewegt und die Logarithmen ja ständig gebraucht werden !_! (ich hab hab mich da jetzt schon lange genug dran vorbei gemogelt).
Es muss auch quantitativ nichts Tolstoi'sches sein, nur brauch ich in dem Punkt dringend Hilfe^^".
Vielen Dank schonmal im Vorraus =).
btw. ist die TEX-Funktion ja mal irre nützlich !_! man lernt nie aus



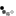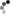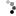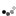
 Zitieren
Zitieren



 ).
).





